.
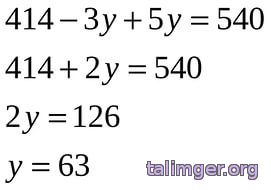 .
Молдабай Ержанов, математика пәнінің
.
Молдабай Ержанов, математика пәнінің
жоғарғы санатты мұғалімі.
№53мектеп-лицейі. Астана қаласы.
Сабақ тақырыбы: «Коши, Коши-Буняковский теңсіздіктерін есеп шығаруда қолдану».
Сынып: 11Ә
Сабақтың мақсаты:Білімділік: оқушы білімін жаңа сатыға көтеру һәм өрістету; тәрбиелік:өскелең ұрпақтың эстетикалық талғам деңгейін шыңдау; дамытушылық;оқушы бойында байқампаздық, қисынды ойлау қабілеттерін қалыптастыру.
Сабақтың жоспары:
1. Қажетті формулалар. Коши теңсіздігі: Егер а_1≥0; а_2≥0,…а_n≥0болса, онда
а_(1+a_(2+⋯+a_n ) )/n≥√(n&a_(1∙) a_2…a_n )
теңсіздігі ақиқат болады.
Ескерту: Қатаң емес теңсіздіктен «теңдік» белгісі а_1=a_2=⋯=a_nболғанда ғана орындалады. Теңсіздіктің n=2 болғандағы дербес жағдайы (а_(1+) a_2)/2≥√(a_1.a_2 )түрінде көрініс табады.
Коши-Буняковский теңсіздігі: Кез-келген x_1;х_2 〖;…;x〗_n және у_1;у_2 〖;…;у〗_n сандар легі үшін мына теңсіздік тура болады:
(х_1 у_2+х_2 у_2+⋯+х_n у_n )^2≤(x_1^2+x_2^2+⋯+x_n^2 )(y_1^2+y_2^2+⋯+y_n^2 ), мұндағы n≥2
.
Ескерту: Мұндағы «теңдік» таңбасы х_к 〖 және у〗_к сандары пропорционал болғанда ғана орындалады.
2. Ұтымды шығарылуы (дәлелденуі) аталмыш формулаларды қарастырған мысалдарлегі.
1-мысал. Кез-келген а≥0үшін 3а^3-6а^2+4≥0 теңсіздігін дәлелдеңдер. а≥0 болған себепті Коши теңсіздігін n=3, болған жағдайында қолдансақ.
3а^3+4=а^3+2а^3+4≥3∛(а^3∙2а^3∙4)=6а^2
Демек, теңсіздік дұрыстығы дәлелденді деген сөз.
2-мысал.а+b+c=1 жағдайында а^2+b^2+c^2≥1/3теңсіздігінің дұрыс болатынын дәлелдеңдер. Коши-Буняковский теңсіздігін ескере отырып мынаны аламыз: 1=(а+b+c)^2=(1.а+1.b+1.c)^2 (≤1^2+1^2+1^2).(a^2+b^2+c^2)=3(a^2+b^2+c^2).Ал бұдан аталмыш теңсіздіктің ақиқаттығы көрініс береді.
3-мысал.а>0,в>0үшін1/a+1/b≥4/(a+b)болатынын дәлелдеңдер.
Коши теңсіздігінің дербес жағдайын 2 рет қолдану төмендегідей нәтиже береді.
1/а+1/b≥2√(1/a∙1/b)=2/√ав≥2/((а+в)/2)=4/(а+в).
4-мысал. Қос теңсіздікті дәлелдеңдер:
-2≤a√(1-b^2 )+b√(1-c^2 )+c√(1-d^2 )+d√(1-a^2 )≤2,
мұндағы
-1≤a≤1;-1≤в≤1;-1≤с≤1;-1≤d≤1.
Коши-Буняковский теңсіздігінқолдану төмендегі нәтижені береді.
(a√(1-b^2 )+b√(1-c^2 )+c√(1-d^2 )+d√(1-a^2 ) )^2≤(a^2+1-c^2+c^2+1-a^2)x
x(〖1-b〗^2+b^2+1-d^2+d^2)=4
осыдан қос теңсіздіктің де тура екендігі шығады.
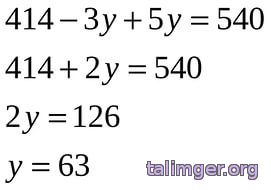
«Коши, Коши-Буняковский теңсіздіктерін есеп шығаруда қолдану».
жоғарғы санатты мұғалімі.
№53мектеп-лицейі. Астана қаласы.
Сабақ тақырыбы: «Коши, Коши-Буняковский теңсіздіктерін есеп шығаруда қолдану».
Сынып: 11Ә
Сабақтың мақсаты:Білімділік: оқушы білімін жаңа сатыға көтеру һәм өрістету; тәрбиелік:өскелең ұрпақтың эстетикалық талғам деңгейін шыңдау; дамытушылық;оқушы бойында байқампаздық, қисынды ойлау қабілеттерін қалыптастыру.
Сабақтың жоспары:
1. Қажетті формулалар. Коши теңсіздігі: Егер а_1≥0; а_2≥0,…а_n≥0болса, онда
а_(1+a_(2+⋯+a_n ) )/n≥√(n&a_(1∙) a_2…a_n )
теңсіздігі ақиқат болады.
Ескерту: Қатаң емес теңсіздіктен «теңдік» белгісі а_1=a_2=⋯=a_nболғанда ғана орындалады. Теңсіздіктің n=2 болғандағы дербес жағдайы (а_(1+) a_2)/2≥√(a_1.a_2 )түрінде көрініс табады.
Коши-Буняковский теңсіздігі: Кез-келген x_1;х_2 〖;…;x〗_n және у_1;у_2 〖;…;у〗_n сандар легі үшін мына теңсіздік тура болады:
(х_1 у_2+х_2 у_2+⋯+х_n у_n )^2≤(x_1^2+x_2^2+⋯+x_n^2 )(y_1^2+y_2^2+⋯+y_n^2 ), мұндағы n≥2
.
Ескерту: Мұндағы «теңдік» таңбасы х_к 〖 және у〗_к сандары пропорционал болғанда ғана орындалады.
2. Ұтымды шығарылуы (дәлелденуі) аталмыш формулаларды қарастырған мысалдарлегі.
1-мысал. Кез-келген а≥0үшін 3а^3-6а^2+4≥0 теңсіздігін дәлелдеңдер. а≥0 болған себепті Коши теңсіздігін n=3, болған жағдайында қолдансақ.
3а^3+4=а^3+2а^3+4≥3∛(а^3∙2а^3∙4)=6а^2
Демек, теңсіздік дұрыстығы дәлелденді деген сөз.
2-мысал.а+b+c=1 жағдайында а^2+b^2+c^2≥1/3теңсіздігінің дұрыс болатынын дәлелдеңдер. Коши-Буняковский теңсіздігін ескере отырып мынаны аламыз: 1=(а+b+c)^2=(1.а+1.b+1.c)^2 (≤1^2+1^2+1^2).(a^2+b^2+c^2)=3(a^2+b^2+c^2).Ал бұдан аталмыш теңсіздіктің ақиқаттығы көрініс береді.
3-мысал.а>0,в>0үшін1/a+1/b≥4/(a+b)болатынын дәлелдеңдер.
Коши теңсіздігінің дербес жағдайын 2 рет қолдану төмендегідей нәтиже береді.
1/а+1/b≥2√(1/a∙1/b)=2/√ав≥2/((а+в)/2)=4/(а+в).
4-мысал. Қос теңсіздікті дәлелдеңдер:
-2≤a√(1-b^2 )+b√(1-c^2 )+c√(1-d^2 )+d√(1-a^2 )≤2,
мұндағы
-1≤a≤1;-1≤в≤1;-1≤с≤1;-1≤d≤1.
Коши-Буняковский теңсіздігінқолдану төмендегі нәтижені береді.
(a√(1-b^2 )+b√(1-c^2 )+c√(1-d^2 )+d√(1-a^2 ) )^2≤(a^2+1-c^2+c^2+1-a^2)x
x(〖1-b〗^2+b^2+1-d^2+d^2)=4
осыдан қос теңсіздіктің де тура екендігі шығады.
Просмотров: 4538
.
